5. Vectors

Vectors are a crucial part of working with picraft; sufficiently important to demand their own section. This chapter introduces all the major vector operations with simple examples and diagrams illustrating the results.

5.1. Vector-vector operations

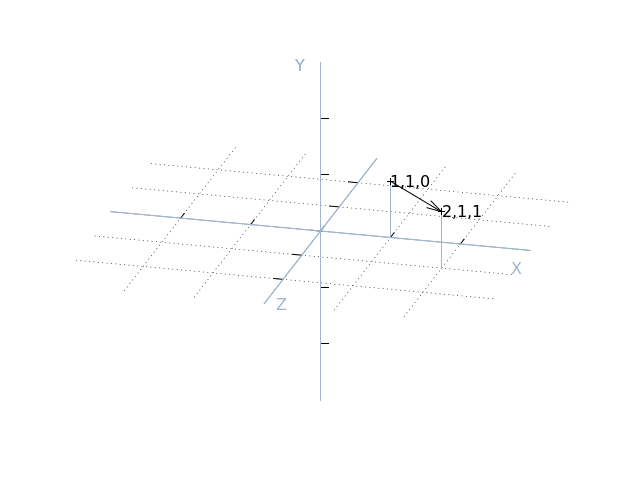
The picraft Vector class is extremely flexible and supports a wide variety of operations. All Python’s built-in operations (addition, subtraction, division, multiplication, modulus, absolute, bitwise operations, etc.) are supported between two vectors, in which case the operation is performed element-wise. In other words, adding two vectors A and B produces a new vector with its x attribute set to A.x + B.x, its y attribute set to A.y + B.y and so on:

>>> from picraft import *
>>> Vector(1, 1, 0) + Vector(1, 0, 1)
Vector(x=2, y=1, z=1)
_images/vector1.png

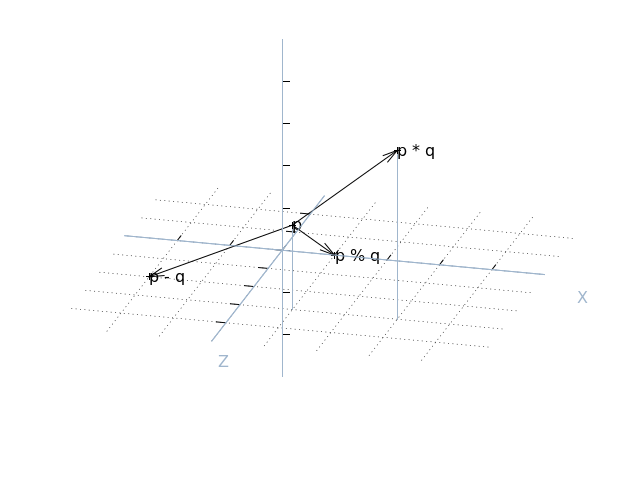
Likewise for subtraction, multiplication, etc.:

>>> p = Vector(1, 2, 3)
>>> q = Vector(3, 2, 1)
>>> p - q
Vector(x=-2, y=0, z=2)
>>> p * q
Vector(x=3, y=4, z=3)
>>> p % q
Vector(x=1, y=0, z=0)
_images/vector2.png

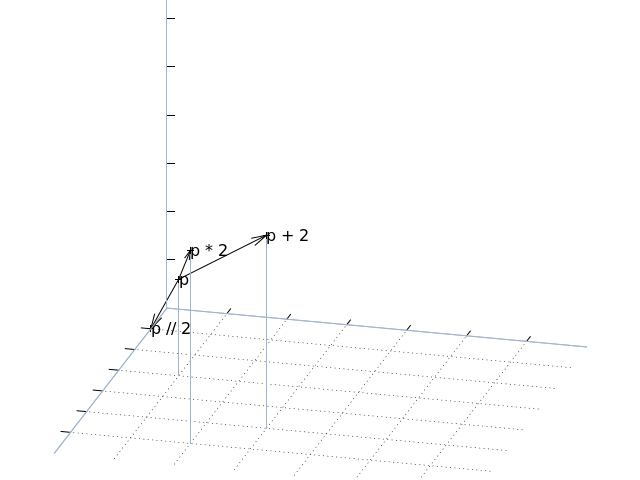
5.2. Vector-scalar operations

Vectors also support several operations between themselves and a scalar value. In this case the operation with the scalar is applied to each element of the vector. For example, multiplying a vector by the number 2 will return a new vector with every element of the original multiplied by 2:

>>> p * 2
Vector(x=2, y=4, z=6)
>>> p + 2
Vector(x=3, y=4, z=5)
>>> p // 2
Vector(x=0, y=1, z=1)
_images/vector3.png

5.3. Miscellaneous function support

Vectors also support several of Python’s built-in functions:

>>> abs(Vector(-1, 0, 1))
Vector(x=1, y=0, z=1)
>>> pow(Vector(1, 2, 3), 2)
Vector(x=1, y=4, z=9)
>>> import math
>>> math.trunc(Vector(1.5, 2.3, 3.7))
Vector(x=1, y=2, z=3)

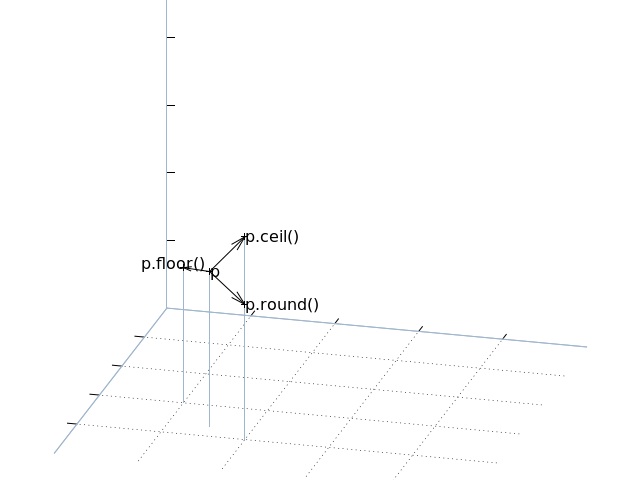
5.4. Vector rounding

Some built-in functions can’t be directly supported, in which case equivalently named methods are provided:

>>> p = Vector(1.5, 2.3, 3.7)
>>> p.round()
Vector(x=2, y=2, z=4)
>>> p.ceil()
Vector(x=2, y=3, z=4)
>>> p.floor()
Vector(x=1, y=2, z=3)
_images/vector4.png

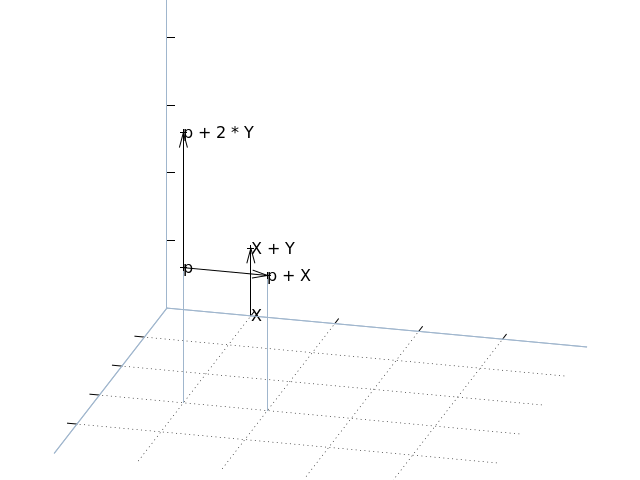
5.5. Short-cuts

Several vector short-hands are also provided. One for the unit vector along each of the three axes (X, Y, and Z), one for the origin (O), and finally V which is simply a short-hand for Vector itself. Obviously, these can be used to simplify many vector-related operations:

>>> X
Vector(x=1, y=0, z=0)
>>> X + Y
Vector(x=1, y=1, z=0)
>>> p = V(1, 2, 3)
>>> p + X
Vector(x=2, y=2, z=3)
>>> p + 2 * Y
Vector(x=1, y=6, z=3)
_images/vector5.png

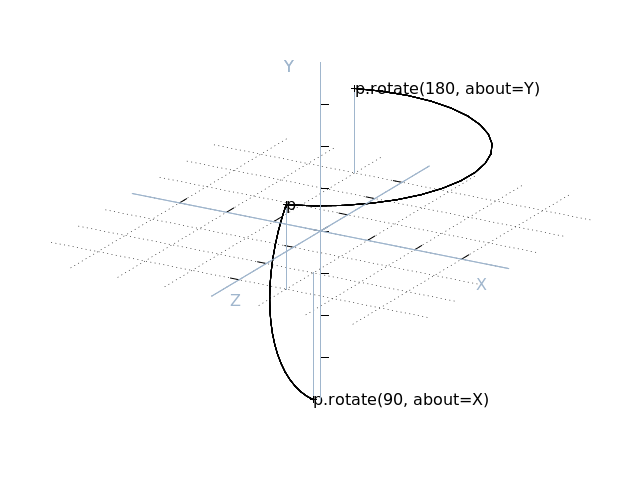
5.6. Rotation

From the paragraphs above it should be relatively easy to see how one can implement vector translation and vector scaling using everyday operations like addition, subtraction, multiplication and divsion. The third major transformation usually required of vectors, rotation, is a little harder. For this, the rotate() method is provided. This takes two mandatory arguments: the number of degrees to rotate, and a vector specifying the axis about which to rotate (it is recommended that this is specified as a keyword argument for code clarity). For example:

>>> p = V(1, 2, 3)
>>> p.rotate(90, about=X)
Vector(x=1.0, y=-3.0, z=2.0)
>>> p.rotate(180, about=Y)
Vector(x=-0.9999999999999997, y=2, z=-3.0)
>>> p.rotate(180, about=Y).round()
Vector(x=-1.0, y=2.0, z=-3.0)
_images/vector6.png 
>>> X.rotate(180, about=X + Y).round()
Vector(x=-0.0, y=1.0, z=-0.0)
_images/vector7.png

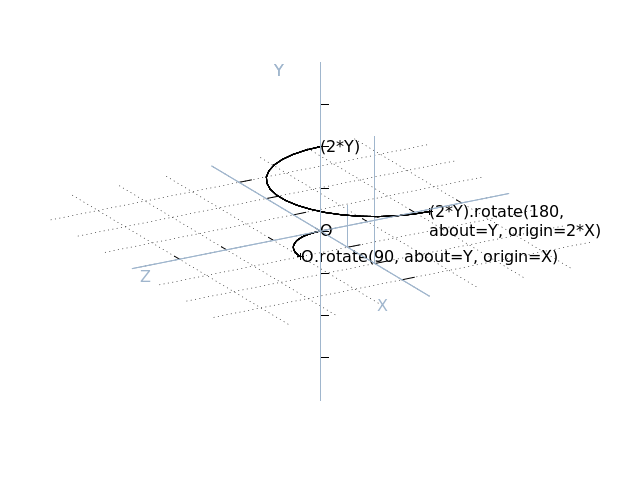
A third optional argument to rotate, origin, permits rotation about an arbitrary line. When specified, the axis of rotation passes through the point specified by origin and runs in the direction of the axis specified by about. Naturally, origin defaults to the origin (0, 0, 0):

>>> (2 * Y).rotate(180, about=Y, origin=2 * X).round()
Vector(x=4.0, y=2.0, z=0.0)
>>> O.rotate(90, about=Y, origin=X).round()
Vector(x=1.0, y=0.0, z=1.0)
_images/vector8.png

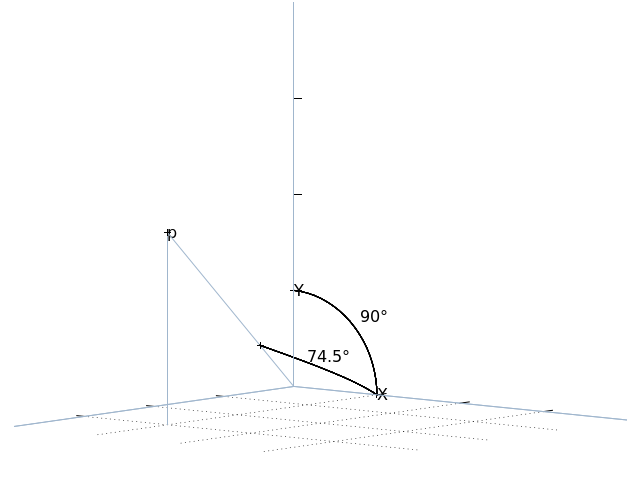
To aid in certain kinds of rotation, the angle_between() method can be used to determine the angle between two vectors (in the plane common to both):

>>> X.angle_between(Y)
90.0
>>> p = V(1, 2, 3)
>>> X.angle_between(p)
74.498640433063
_images/vector9.png

5.7. Magnitudes

The magnitude attribute can be used to determine the length of a vector (via Pythagoras’ theorem, while the unit attribute can be used to obtain a vector in the same direction with a magnitude (length) of 1.0. The distance_to() method can also be used to calculate the distance between two vectors (this is simply equivalent to the magnitude of the vector obtained by subtracting one vector from the other):

>>> p = V(1, 2, 3)
>>> p.magnitude
3.7416573867739413
>>> p.unit
Vector(x=0.2672612419124244, y=0.5345224838248488, z=0.8017837257372732)
>>> p.unit.magnitude
1.0
>>> q = V(2, 0, 1)
>>> p.distance_to(q)
3.0
_images/vector10.png

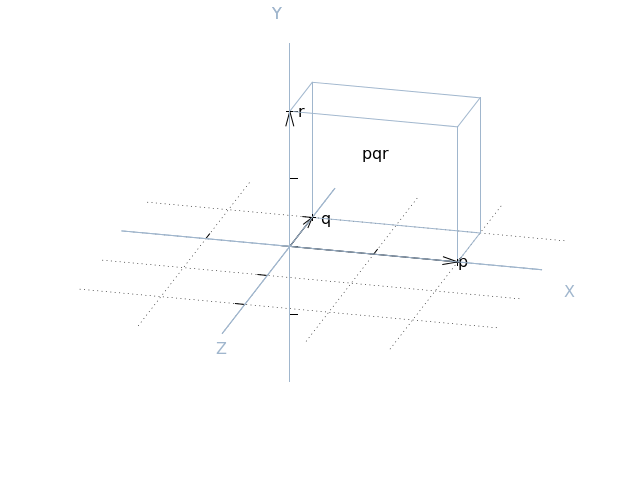
5.8. Dot and cross products

The dot and cross products of a vector with another can be calculated using the dot() and cross() methods respectively. These are useful for determining whether vectors are orthogonal (the dot product of orthogonal vectors is always 0), for finding a vector perpendicular to the plane of two vectors (via the cross product), or for finding the volume of a parallelepiped defined by three vectors, via the triple product:

>>> p = V(x=2)
>>> q = V(z=-1)
>>> p.dot(q)
0
>>> r = p.cross(q)
>>> r
Vector(x=0, y=2, z=0)
>>> area_of_pqr = p.cross(q).dot(r)
>>> area_of_pqr
4
_images/vector11.png

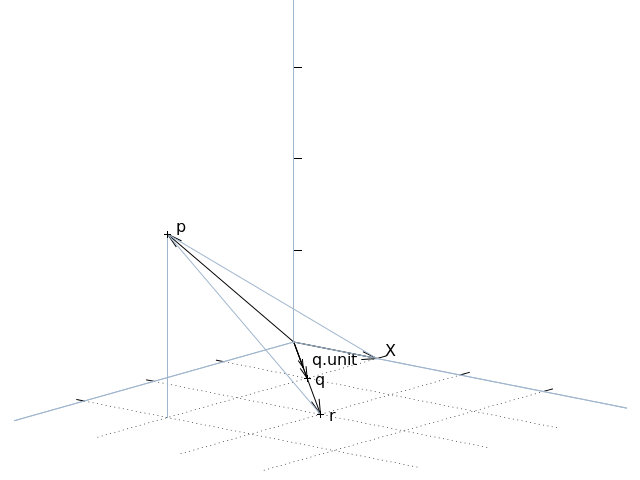
5.9. Projection

The final method provided by the Vector class is project() which implements scalar projection. You might think of this as calculating the length of the shadow one vector casts upon another. Or, put another way, this is the length of one vector in the direction of another (unit) vector:

>>> p = V(1, 2, 3)
>>> p.project(X)
1.0
>>> q = X + Z
>>> p.project(q)
2.82842712474619
>>> r = q.unit * p.project(q)
>>> r.round(4)
Vector(x=2.0, y=0.0, z=2.0)
_images/vector12.png